12. They Called It LISP for a Reason: List Processing

Lists play an important role in Lisp—for reasons both historical and practical. Historically, lists were Lisp's original composite data type, though it has been decades since they were its only such data type. These days, a Common Lisp programmer is as likely to use a vector, a hash table, or a user-defined class or structure as to use a list.

Practically speaking, lists remain in the language because they're an excellent solution to certain problems. One such problem—how to represent code as data in order to support code-transforming and code-generating macros—is particular to Lisp, which may explain why other languages don't feel the lack of Lisp-style lists. More generally, lists are an excellent data structure for representing any kind of heterogeneous and/or hierarchical data. They're also quite lightweight and support a functional style of programming that's another important part of Lisp's heritage.

Thus, you need to understand lists on their own terms; as you gain a better understanding of how lists work, you'll be in a better position to appreciate when you should and shouldn't use them.

Spoon Boy: Do not try and bend the list. That's impossible. Instead . . . only try to realize the truth.

Neo: What truth?

Spoon Boy: There is no list.

Neo: There is no list?

Spoon Boy: Then you'll see that it is not the list that bends; it is only yourself.¹

The key to understanding lists is to understand that they're largely an illusion built on top of objects that are instances of a more primitive data type. Those simpler objects are pairs of values called cons cells, after the function CONS used to create them.

CONS takes two arguments and returns a new cons cell containing the two values.² These values can be references to any kind of object. Unless the second value is NIL or another cons cell, a cons is printed as the two values in parentheses separated by a dot, a so-called dotted pair.

(cons 1 2) ==> (1 . 2)

The two values in a cons cell are called the CAR and the CDR after the names of the functions used to access them. At the dawn of time, these names were mnemonic, at least to the folks implementing the first Lisp on an IBM 704. But even then they were just lifted from the assembly mnemonics used to implement the operations. However, it's not all bad that these names are somewhat meaningless—when considering individual cons cells, it's best to think of them simply as an arbitrary pair of values without any particular semantics. Thus:

(car (cons 1 2)) ==> 1
(cdr (cons 1 2)) ==> 2

Both CAR and CDR are also SETFable places—given an existing cons cell, it's possible to assign a new value to either of its values.³

(defparameter *cons* (cons 1 2))
*cons*                 ==> (1 . 2)
(setf (car *cons*) 10) ==> 10
*cons*                 ==> (10 . 2)
(setf (cdr *cons*) 20) ==> 20
*cons*                 ==> (10 . 20)

Because the values in a cons cell can be references to any kind of object, you can build larger structures out of cons cells by linking them together. Lists are built by linking together cons cells in a chain. The elements of the list are held in the CARs of the cons cells while the links to subsequent cons cells are held in the CDRs. The last cell in the chain has a CDR of NIL, which—as I mentioned in Chapter 4—represents the empty list as well as the boolean value false.

This arrangement is by no means unique to Lisp; it's called a singly linked list. However, few languages outside the Lisp family provide such extensive support for this humble data type.

So when I say a particular value is a list, what I really mean is it's either NIL or a reference to a cons cell. The CAR of the cons cell is the first item of the list, and the CDR is a reference to another list, that is, another cons cell or NIL, containing the remaining elements. The Lisp printer understands this convention and prints such chains of cons cells as parenthesized lists rather than as dotted pairs.

(cons 1 nil)                   ==> (1)
(cons 1 (cons 2 nil))          ==> (1 2)
(cons 1 (cons 2 (cons 3 nil))) ==> (1 2 3)

When talking about structures built out of cons cells, a few diagrams can be a big help. Box-and-arrow diagrams represent cons cells as a pair of boxes like this:

The box on the left represents the CAR, and the box on the right is the CDR. The values stored in a particular cons cell are either drawn in the appropriate box or represented by an arrow from the box to a representation of the referenced value.⁴ For instance, the list (1 2 3), which consists of three cons cells linked together by their CDRs, would be diagrammed like this:

However, most of the time you work with lists you won't have to deal with individual cons cells—the functions that create and manipulate lists take care of that for you. For example, the LIST function builds a cons cells under the covers for you and links them together; the following LIST expressions are equivalent to the previous CONS expressions:

(list 1)     ==> (1)
(list 1 2)   ==> (1 2)
(list 1 2 3) ==> (1 2 3)

Similarly, when you're thinking in terms of lists, you don't have to use the meaningless names CAR and CDR; FIRST and REST are synonyms for CAR and CDR that you should use when you're dealing with cons cells as lists.

(defparameter *list* (list 1 2 3 4))
(first *list*)        ==> 1
(rest *list*)         ==> (2 3 4)
(first (rest *list*)) ==> 2

Because cons cells can hold any kind of values, so can lists. And a single list can hold objects of different types.

(list "foo" (list 1 2) 10) ==> ("foo" (1 2) 10)

The structure of that list would look like this:

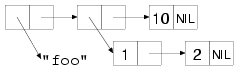
Because lists can have other lists as elements, you can also use them to represent trees of arbitrary depth and complexity. As such, they make excellent representations for any heterogeneous, hierarchical data. Lisp-based XML processors, for instance, usually represent XML documents internally as lists. Another obvious example of tree-structured data is Lisp code itself. In Chapters 30 and 31 you'll write an HTML generation library that uses lists of lists to represent the HTML to be generated. I'll talk more next chapter about using cons cells to represent other data structures.

Common Lisp provides quite a large library of functions for manipulating lists. In the sections "List-Manipulation Functions" and "Mapping," you'll look at some of the more important of these functions. However, they will be easier to understand in the context of a few ideas borrowed from functional programming.

The essence of functional programming is that programs are built entirely of functions with no side effects that compute their results based solely on the values of their arguments. The advantage of the functional style is that it makes programs easier to understand. Eliminating side effects eliminates almost all possibilities for action at a distance. And since the result of a function is determined only by the values of its arguments, its behavior is easier to understand and test. For instance, when you see an expression such as (+ 3 4), you know the result is uniquely determined by the definition of the + function and the values 3 and 4. You don't have to worry about what may have happened earlier in the execution of the program since there's nothing that can change the result of evaluating that expression.

Functions that deal with numbers are naturally functional since numbers are immutable. A list, on the other hand, can be mutated, as you've just seen, by SETFing the CARs and CDRs of the cons cells that make up its backbone. However, lists can be treated as a functional data type if you consider their value to be determined by the elements they contain. Thus, any list of the form (1 2 3 4) is functionally equivalent to any other list containing those four values, regardless of what cons cells are actually used to represent the list. And any function that takes a list as an argument and returns a value based solely on the contents of the list can likewise be considered functional. For instance, the REVERSE sequence function, given the list (1 2 3 4), always returns a list (4 3 2 1). Different calls to REVERSE with functionally equivalent lists as the argument will return functionally equivalent result lists. Another aspect of functional programming, which I'll discuss in the section "Mapping," is the use of higher-order functions: functions that treat other functions as data, taking them as arguments or returning them as results.

Most of Common Lisp's list-manipulation functions are written in a functional style. I'll discuss later how to mix functional and other coding styles, but first you should understand a few subtleties of the functional style as applied to lists.

The reason most list functions are written functionally is it allows them to return results that share cons cells with their arguments. To take a concrete example, the function APPEND takes any number of list arguments and returns a new list containing the elements of all its arguments. For instance:

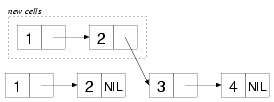
(append (list 1 2) (list 3 4)) ==> (1 2 3 4)

From a functional point of view, APPEND's job is to return the list (1 2 3 4) without modifying any of the cons cells in the lists (1 2) and (3 4). One obvious way to achieve that goal is to create a completely new list consisting of four new cons cells. However, that's more work than is necessary. Instead, APPEND actually makes only two new cons cells to hold the values 1 and 2, linking them together and pointing the CDR of the second cons cell at the head of the last argument, the list (3 4). It then returns the cons cell containing the 1. None of the original cons cells has been modified, and the result is indeed the list (1 2 3 4). The only wrinkle is that the list returned by APPEND shares some cons cells with the list (3 4). The resulting structure looks like this:

In general, APPEND must copy all but its last argument, but it can always return a result that shares structure with the last argument.

Other functions take similar advantage of lists' ability to share structure. Some, like APPEND, are specified to always return results that share structure in a particular way. Others are simply allowed to return shared structure at the discretion of the implementation.

If Common Lisp were a purely functional language, that would be the end of the story. However, because it's possible to modify a cons cell after it has been created by SETFing its CAR or CDR, you need to think a bit about how side effects and structure sharing mix.

Because of Lisp's functional heritage, operations that modify existing objects are called destructive—in functional programming, changing an object's state "destroys" it since it no longer represents the same value. However, using the same term to describe all state-modifying operations leads to a certain amount of confusion since there are two very different kinds of destructive operations, for-side-effect operations and recycling operations.⁵

For-side-effect operations are those used specifically for their side effects. All uses of SETF are destructive in this sense, as are functions that use SETF under the covers to change the state of an existing object such as VECTOR-PUSH or VECTOR-POP. But it's a bit unfair to describe these operations as destructive—they're not intended to be used in code written in a functional style, so they shouldn't be described using functional terminology. However, if you mix nonfunctional, for-side-effect operations with functions that return structure-sharing results, then you need to be careful not to inadvertently modify the shared structure. For instance, consider these three definitions:

(defparameter *list-1* (list 1 2))
(defparameter *list-2* (list 3 4))
(defparameter *list-3* (append *list-1* *list-2*))

After evaluating these forms, you have three lists, but *list-3* and *list-2* share structure just like the lists in the previous diagram.

*list-1*                  ==> (1 2)
*list-2*                  ==> (3 4)
*list-3*                  ==> (1 2 3 4)

Now consider what happens when you modify *list-2*.

(setf (first *list-2*) 0) ==> 0
*list-2*                  ==> (0 4)     ; as expected
*list-3*                  ==> (1 2 0 4) ; maybe not what you wanted

The change to *list-2* also changes *list-3* because of the shared structure: the first cons cell in *list-2* is also the third cons cell in *list-3*. SETFing the FIRST of *list-2* changes the value in the CAR of that cons cell, affecting both lists.

On the other hand, the other kind of destructive operations, recycling operations, are intended to be used in functional code. They use side effects only as an optimization. In particular, they reuse certain cons cells from their arguments when building their result. However, unlike functions such as APPEND that reuse cons cells by including them, unmodified, in the list they return, recycling functions reuse cons cells as raw material, modifying the CAR and CDR as necessary to build the desired result. Thus, recycling functions can be used safely only when the original lists aren't going to be needed after the call to the recycling function.

To see how a recycling function works, let's compare REVERSE, the nondestructive function that returns a reversed version of a sequence, to NREVERSE, a recycling version of the same function. Because REVERSE doesn't modify its argument, it must allocate a new cons cell for each element in the list being reversed. But suppose you write something like this:

(setf *list* (reverse *list*))

By assigning the result of REVERSE back to *list*, you've removed the reference to the original value of *list*. Assuming the cons cells in the original list aren't referenced anywhere else, they're now eligible to be garbage collected. However, in many Lisp implementations it'd be more efficient to immediately reuse the existing cons cells rather than allocating new ones and letting the old ones become garbage.

NREVERSE allows you to do exactly that. The N stands for non-consing, meaning it doesn't need to allocate any new cons cells. The exact side effects of NREVERSE are intentionally not specified—it's allowed to modify any CAR or CDR of any cons cell in the list—but a typical implementation might walk down the list changing the CDR of each cons cell to point to the previous cons cell, eventually returning the cons cell that was previously the last cons cell in the old list and is now the head of the reversed list. No new cons cells need to be allocated, and no garbage is created.

Most recycling functions, like NREVERSE, have nondestructive counterparts that compute the same result. In general, the recycling functions have names that are the same as their non-destructive counterparts except with a leading N. However, not all do, including several of the more commonly used recycling functions such as NCONC, the recycling version of APPEND, and DELETE, DELETE-IF, DELETE-IF-NOT, and DELETE-DUPLICATES, the recycling versions of the REMOVE family of sequence functions.

In general, you use recycling functions in the same way you use their nondestructive counterparts except it's safe to use them only when you know the arguments aren't going to be used after the function returns. The side effects of most recycling functions aren't specified tightly enough to be relied upon.

However, the waters are further muddied by a handful of recycling functions with specified side effects that can be relied upon. They are NCONC, the recycling version of APPEND, and NSUBSTITUTE and its -IF and -IF-NOT variants, the recycling versions of the sequence functions SUBSTITUTE and friends.

Like APPEND, NCONC returns a concatenation of its list arguments, but it builds its result in the following way: for each nonempty list it's passed, NCONC sets the CDR of the list's last cons cell to point to the first cons cell of the next nonempty list. It then returns the first list, which is now the head of the spliced-together result. Thus:

(defparameter *x* (list 1 2 3))

(nconc *x* (list 4 5 6)) ==> (1 2 3 4 5 6)

*x* ==> (1 2 3 4 5 6)

NSUBSTITUTE and variants can be relied on to walk down the list structure of the list argument and to SETF the CARs of any cons cells holding the old value to the new value and to otherwise leave the list intact. It then returns the original list, which now has the same value as would've been computed by SUBSTITUTE. ⁶

The key thing to remember about NCONC and NSUBSTITUTE is that they're the exceptions to the rule that you can't rely on the side effects of recycling functions. It's perfectly acceptable—and arguably good style—to ignore the reliability of their side effects and use them, like any other recycling function, only for the value they return.

Although you can use recycling functions whenever the arguments to the recycling function won't be used after the function call, it's worth noting that each recycling function is a loaded gun pointed footward: if you accidentally use a recycling function on an argument that is used later, you're liable to lose some toes.

To make matters worse, shared structure and recycling functions tend to work at cross-purposes. Nondestructive list functions return lists that share structure under the assumption that cons cells are never modified, but recycling functions work by violating that assumption. Or, put another way, sharing structure is based on the premise that you don't care exactly what cons cells make up a list while using recycling functions requires that you know exactly what cons cells are referenced from where.

In practice, recycling functions tend to be used in a few idiomatic ways. By far the most common recycling idiom is to build up a list to be returned from a function by "consing" onto the front of a list, usually by PUSHing elements onto a list stored in a local variable and then returning the result of NREVERSEing it.⁷

This is an efficient way to build a list because each PUSH has to create only one cons cell and modify a local variable and the NREVERSE just has to zip down the list reassigning the CDRs. Because the list is created entirely within the function, there's no danger any code outside the function has a reference to any of its cons cells. Here's a function that uses this idiom to build a list of the first n numbers, starting at zero:⁸

(defun upto (max)
  (let ((result nil))
    (dotimes (i max)
      (push i result))
    (nreverse result)))

(upto 10) ==> (0 1 2 3 4 5 6 7 8 9)

The next most common recycling idiom⁹ is to immediately reassign the value returned by the recycling function back to the place containing the potentially recycled value. For instance, you'll often see expressions like the following, using DELETE, the recycling version of REMOVE:

(setf foo (delete nil foo))

This sets the value of foo to its old value except with all the NILs removed. However, even this idiom must be used with some care—if foo shares structure with lists referenced elsewhere, using DELETE instead of REMOVE can destroy the structure of those other lists. For example, consider the two lists *list-2* and *list-3* from earlier that share their last two cons cells.

*list-2* ==> (0 4)
*list-3* ==> (1 2 0 4)

You can delete 4 from *list-3* like this:

(setf *list-3* (delete 4 *list-3*)) ==> (1 2 0)

However, DELETE will likely perform the necessary deletion by setting the CDR of the third cons cell to NIL, disconnecting the fourth cons cell, the one holding the 4, from the list. Because the third cons cell of *list-3* is also the first cons cell in *list-2*, the following modifies *list-2* as well:

*list-2* ==> (0)

If you had used REMOVE instead of DELETE, it would've built a list containing the values 1, 2, and 0, creating new cons cells as necessary rather than modifying any of the cons cells in *list-3*. In that case, *list-2* wouldn't have been affected.

The PUSH/NREVERSE and SETF/DELETE idioms probably account for 80 percent of the uses of recycling functions. Other uses are possible but require keeping careful track of which functions return shared structure and which do not.

In general, when manipulating lists, it's best to write your own code in a functional style—your functions should depend only on the contents of their list arguments and shouldn't modify them. Following that rule will, of course, rule out using any destructive functions, recycling or otherwise. Once you have your code working, if profiling shows you need to optimize, you can replace nondestructive list operations with their recycling counterparts but only if you're certain the argument lists aren't referenced from anywhere else.

One last gotcha to watch out for is that the sorting functions SORT, STABLE-SORT, and MERGE mentioned in Chapter 11 are also recycling functions when applied to lists.¹⁰ However, these functions don't have nondestructive counterparts, so if you need to sort a list without destroying it, you need to pass the sorting function a copy made with COPY-LIST. In either case you need to be sure to save the result of the sorting function because the original argument is likely to be in tatters. For instance:

CL-USER> (defparameter *list* (list 4 3 2 1))
*LIST*
CL-USER> (sort *list* #'<)
(1 2 3 4)                      ; looks good
CL-USER> *list*
(4)                            ; whoops!

With that background out of the way, you're ready to look at the library of functions Common Lisp provides for manipulating lists.

You've already seen the basic functions for getting at the elements of a list: FIRST and REST. Although you can get at any element of a list by combining enough calls to REST (to move down the list) with a FIRST (to extract the element), that can be a bit tedious. So Common Lisp provides functions named for the other ordinals from SECOND to TENTH that return the appropriate element. More generally, the function NTH takes two arguments, an index and a list, and returns the nth (zero-based) element of the list. Similarly, NTHCDR takes an index and a list and returns the result of calling CDR n times. (Thus, (nthcdr 0 ...A token consisting solely of multiple dots is illegal.) simply returns the original list, and (nthcdr 1 ...A token consisting solely of multiple dots is illegal.) is equivalent to REST.) Note, however, that none of these functions is any more efficient, in terms of work done by the computer, than the equivalent combinations of FIRSTs and RESTs—there's no way to get to the nth element of a list without following n CDR references.¹¹

The 28 composite CAR/CDR functions are another family of functions you may see used from time to time. Each function is named by placing a sequence of up to four As and Ds between a C and R, with each A representing a call to CAR and each D a call to CDR. Thus:

(caar list) === (car (car list))
(cadr list) === (car (cdr list))
(cadadr list) === (car (cdr (car (cdr list))))

Note, however, that many of these functions make sense only when applied to lists that contain other lists. For instance, CAAR extracts the CAR of the CAR of the list it's given; thus, the list it's passed must contain another list as its first element. In other words, these are really functions on trees rather than lists:

(caar (list 1 2 3))                  ==> error
(caar (list (list 1 2) 3))           ==> 1
(cadr (list (list 1 2) (list 3 4)))  ==> (3 4)
(caadr (list (list 1 2) (list 3 4))) ==> 3

These functions aren't used as often now as in the old days. And even the most die-hard old-school Lisp hackers tend to avoid the longer combinations. However, they're used quite a bit in older Lisp code, so it's worth at least understanding how they work.¹²

The FIRST-TENTH and CAR, CADR, and so on, functions can also be used as SETFable places if you're using lists nonfunctionally.

Table 12-1 summarizes some other list functions that I won't cover in detail.

Another important aspect of the functional style is the use of higher-order functions, functions that take other functions as arguments or return functions as values. You saw several examples of higher-order functions, such as MAP, in the previous chapter. Although MAP can be used with both lists and vectors (that is, with any kind of sequence), Common Lisp also provides six mapping functions specifically for lists. The differences between the six functions have to do with how they build up their result and whether they apply the function to the elements of the list or to the cons cells of the list structure.

MAPCAR is the function most like MAP. Because it always returns a list, it doesn't require the result-type argument MAP does. Instead, its first argument is the function to apply, and subsequent arguments are the lists whose elements will provide the arguments to the function. Otherwise, it behaves like MAP: the function is applied to successive elements of the list arguments, taking one element from each list per application of the function. The results of each function call are collected into a new list. For example:

(mapcar #'(lambda (x) (* 2 x)) (list 1 2 3)) ==> (2 4 6)
(mapcar #'+ (list 1 2 3) (list 10 20 30)) ==> (11 22 33)

MAPLIST is just like MAPCAR except instead of passing the elements of the list to the function, it passes the actual cons cells.¹³ Thus, the function has access not only to the value of each element of the list (via the CAR of the cons cell) but also to the rest of the list (via the CDR).

MAPCAN and MAPCON work like MAPCAR and MAPLIST except for the way they build up their result. While MAPCAR and MAPLIST build a completely new list to hold the results of the function calls, MAPCAN and MAPCON build their result by splicing together the results—which must be lists—as if by NCONC. Thus, each function invocation can provide any number of elements to be included in the result.¹⁴ MAPCAN, like MAPCAR, passes the elements of the list to the mapped function while MAPCON, like MAPLIST, passes the cons cells.

Finally, the functions MAPC and MAPL are control constructs disguised as functions—they simply return their first list argument, so they're useful only when the side effects of the mapped function do something interesting. MAPC is the cousin of MAPCAR and MAPCAN while MAPL is in the MAPLIST/MAPCON family.

While cons cells and lists are typically considered to be synonymous, that's not quite right—as I mentioned earlier, you can use lists of lists to represent trees. Just as the functions discussed in this chapter allow you to treat structures built out of cons cells as lists, other functions allow you to use cons cells to represent trees, sets, and two kinds of key/value maps. I'll discuss some of those functions in the next chapter.

(when (> x 10) (print x))

;; the condition
(cadr '(when (> x 10) (print x))) ==> (> X 10)

;; the body, as a list
(cddr '(when (> x 10) (print x))) ==> ((PRINT X))

(mapcan #'(lambda (x) (if (= x 10) nil (list x)))  list) === (remove 10 list)